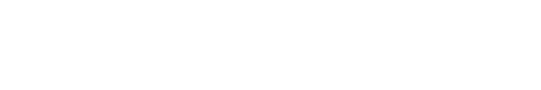Modulators: Introduction, definition of terms

Mini-Circuits offers QPSK (quadrature phase-shift keying) and I&Q modulators from 10% bandwidth to as much as 5:1 octave span. So there's no longer any need to gather double-balanced mixers and 0° and 90° hybrids to assemble "in-house" QPSK or l&Q modulators.

QPSK modulators basically provide constant amplitude, 90° vectors: 0°, 90°, 180°, 270°. I&Q modulators provide variable amplitude 90° vectors and therefore must be specified for linear operation, namely 1 dB compression and harmonic suppression.

Using two recently-patented innovative designs, lengthy and tedious tuning steps associated with conventional manufacturing techniques are absent making these models extremely competitive for low-cost, high volume requirements. Mini-Circuits' 90° phase modulators offer tight unit-to-unit repeatability and excellent performance stability over a -55° to +100°C temperature span.

Units are capable of meeting MIL-M-28837 and MIL-STD-202 electrical and environmental specifications. All I&Q modulators are statistically specified for conversion loss X̄ and σ.

Applications include high-speed data systems, high-performance, low-budget communications systems, and simplified instrumentation to check a variety of narrowband QPSK modulators. Multi-octave and narrowband models are available, for immediate delivery, in hermetically-sealed cases with flat-pack or plug-in versions.

In addition to the models shown in the handbook, Mini-Circuits offers designs for other frequencies, specifications, and package styles including surface-mount. Our experienced engineering group has developed a new technique to enable rapid turn around of new designs, many in less than two weeks.

For a detailed discussion of I&Q applications, see the article that follows "Novel Measurement Schemes Serve I/Q Applications."

Modern Definition of Terms

Quadrature phase shift keying modulator

Quadrature phase-shift-keying (QPSK) modulators are four-port devices with RF-in, RF-out, and two data input ports. A bipolar pulse signal is applied at data ports to produce an RF output signal phase-modulated by 0 (reference), 90, 180, or 270 degrees, depending on the state of the modulating signal.

Insertion loss

The insertion loss of a phase modulator is measured statically in one of the possible four states and represents the worst-case loss for any state. For QPSK modulators, the insertion loss is 6dB typically.

VSWR

VSWR is a measure of impedance match at input and output ports of the modulator. This parameter represents imperfect input and output impedances. Mini-Circuits' modulators have a VSWR of 1.3:1 typically.

Amplitude unbalance

Amplitude unbalance is a measure of the worst-case variation in insertion loss between the four states in a QPSK modulator.

Phase unbalance

Phase unbalance is a measure of the offset from the desired carrier phase relative to the actual phase shift in any of the possible phase states. This is measured with respect to a reference or 0 degree phase state. In MCL catalog specifications, the reference is at the 0 degree phase state with + 20 mA for both control ports.

1 dB compression

As RF signal input level is increased, output should follow in a linear manner. However, after a certain point, output signal level increases at a lower rate until the modulator output level becomes fairly constant. The RF input level for which the output level deviates from linearity by 1 dB is termed the "1 dB compression point".

Novel Measurement Schemes Serve I/Q Applications (In-Phase/quadrature network characteristics can be measured using spectrum or network analyzers)

In-phase/quadrature (I/Q) modulator/demodulator schemes are often used in digital communication systems. The popular form of an I/Q modulator/demodulator consists of a90-deg. splitter, two double-balanced mixers, and a 0-deg. splitter/combiner (Fig. 1). A variety of test methods unique to I/Q networks can be used to provide accurate network characterizations.

An RF signal can be represented in polar coordinates by magnitude and phase, or in x-y coordinates as magnitudes of x and y vectors. In digital radio terminology, x is replaced by I and Y is replaced by Q, hence the name I/Q modulator/ demodulator. The quadrature signals are generated by the 90-deg. hybrid. The I/Q signal's magnitude and polarity determine the translated magnitude and phase of the I/Q vector (modulated RF carrier).

Among the various modulation methods is binary phase-shift keying (BPSK), where the carrier phase is shifted 180 deg. to transmit a change of state from 0 to 1, or vice-versa. In the I/Q plane used to describe the signal graphically, this can be represented by two dots on the I axis spaced equally apart from the origin. Assuming an arbitrary amplitude level of 1 for the RF signal, 1 is represented by a dot with a value of +1 on the I axis, while 0 is represented by a -1 on the I axis. The two states are separated by 180 deg. and the magnitude of the carrier is kept constant. Hence, the rate of change of the phase is the same as the rate of change of the digital bits (or bit rate).

In quadrature phase-shift keying (QPSK), the carrier is shifted in 90 deg. steps. There are four possible phase states, and the magnitude is constant. In I/Q networks, this is achieved by adding the appropriate values of the I and Q vectors. For example, the values of I and Q vectors are +1and +1 for the state "00" and -1 and +1 for state "01", etc. In digital communication, the phase states are called "symbols."

In QPSK modulation, two successive bits are paired to form a symbol. The rate of change of the phase states (or symbol rate) is half of the bit rate. Theoretically, twice the information can be transmitted in a given bandwidth compared to BPSK.

In 8-PSK, there are eight possible phase states, 45 deg. apart, in the I/Q plane. Each phase state or symbol is composed of three bits. Hence, the symbol rate is one third of the bit rate. Note that in 8-PSK, the magnitudes of I and Q vectors are not equal, but the resultant carrier has a constant magnitude.

In 16-quadrature amplitude modulation (QAM), there are 16 phase states in the I/Q plane. Here the carrier magnitude differs for varying phase states; hence, the name QAM. Each symbol represents four bits, so the symbol rate is one fourth of the bit rate.

By extending this reasoning, it can be stated that the symbol rates for 64-QAM and 256-QAMare one-sixth and one-eighth of the bit rate, respectively. In practice, this is not the case. Realizable bit rates are lower than theoretical values due to various considerations. For higher-order QAM, the separation between phase states becomes smaller and susceptibility to noise becomes greater. In order to realize higher-order QAM, the signal-to-noise ratio (SNR)should be increased. Also, mixers should operate in the linear range to preserve symbol spacing.

Digital Modulator

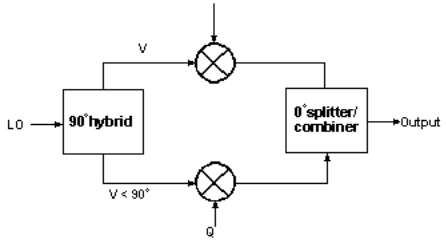
The principle component of a digital modulator (Fig. 2a) is the 90-deg. splitter, which splits the carrier into two equal parts which are 90 deg. out of phase. An incoming analog signal is converted into digital form by an analog-to-digital converter(ADC) and is fed to a map/coder. The map takes the serial data, groups it into symbols, and produces I and Q outputs of suitable amplitude and polarity for each symbol. The I and Q signals are then fed to the mixer I and Q ports, which generate double-sideband outputs that are in quadrature. These outputs are summed in a 0-deg. hybrid, and the resultant output is an I/Q-modulated signal.

In a demodulator (Fig. 2b), the carrier is recovered from the incoming modulated signal and fed to 90° hybrid and modulated signal to the 0° hybrids. The I and Q ports contain the down converted intermediate-frequency (IF) signal. The I and Q outputs are then fed to a regenerator and decoder to obtain the demodulated signal.

Switched QPSK

A switched QPSK modulator is similar to an I/Q modulator. Its mixers are normally driven with bipolar ±20-mA signals at the I and Q ports. This results in a 0- or 180-deg. phase shift of the signal applied to each mixer, but with a constant output magnitude. The mixer outputs are combined in a 0-deg. hybrid. Radio-frequency (RF) input to this network should he below the 1-dB compression level. This network is excellent for QPSK applications at frequencies up to the gigahertz range, provided that amplitude, phase balance, and impedance match be maintained in the mixers and hybrids. However, the mixers are operated as switches and are not linear. Therefore, this mode of operation is not suitable for QAM.

Important I/Q network specifications include:

• amplitude and phase imbalance
• conversion loss
• carrier and single-sideband rejection
• port-to-port isolation
• third- and fifth-order products
• DC offset

In an ideal I/Q demodulator, the LO signal is split into two equal-amplitude signals which are 90 deg. apart, and the RF signal is split into two equal-amplitude, equal-phase signals which are applied to the two mixers. The down converted signals from the two mixers are of equal amplitude but differ in phase by 90 deg. In practice, all four components of the I/Q network deviate from ideal operation. This results in I/Q-port signals that differ in amplitude and phase quadrature. For instance, if two quadrature signals Vi and Vq are given by:

  1a) V_i = A₁ |0

  1b) V_q = A₂ |(90 + Ø)

then amplitude imbalance (in dB) and phase imbalance (in deg.) are defined as:

  2a) 20log A₁/A₂

  2b) Ø deg

Imbalance Testing

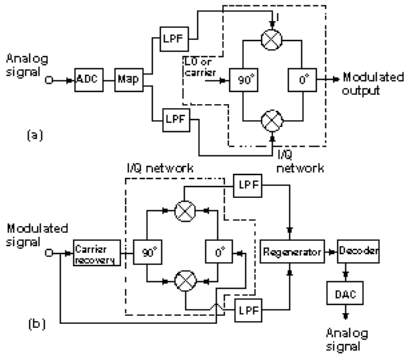
Amplitude and phase imbalances can be measured using a network analyzer in mixer mode (Fig.3). In mixer mode, the network analyzer needs an external IF signal to phase-lock its internal oscillators. This is accomplished by first dividing the LO and RF signals in the two splitters. The resultant signals are applied to the reference mixer and device under test (DUT). The IF output of the reference mixer is filtered to remove the upper sideband and is applied to the analyzer R channel to phase-lock the oscillator. Similar filtering is done to the I-port output of the DUT, which is applied to the analyzer A channel. The A channel then indicates the amplitude of the I-port signal with an arbitrary phase. The analyzer is normalized at this setting. The Q-port termination and the I-port attenuator-filter combination on the I port are then interchanged. The display on the A-channel then becomes the amplitude imbalance and phase difference. The deviation of this phase from 90 deg. is the phase imbalance. For example, if the display reads 89 deg., the phase imbalance is 1 deg.

The A-channel display before normalization indicates the absolute value of the I-port output. Knowing the loss of the attenuator and filter, the conversion loss can be computed. Network analyzers should be calibrated with a power meter to improve accuracy.

The DUT and reference mixer are padded on all ports to improve matching. Too much padding should be avoided or else the power output needed from the network analyzer to obtain a given DUT input would have to be increased. This results in an increased harmonic level from the network analyzer and greater inaccuracy. Padding of 6 to 10 dB is adequate for most measurements. The same precaution regarding allowable loss applies when choosing the two splitters.

In modulator applications, the amplitude and phase imbalance of the I and Q networks have a direct effect on sideband rejection. The output of each mixer is a double-sideband signal. The mixer outputs differ slightly in amplitude due to imbalance in the quadrature hybrid output and the unequal conversion loss and phase response of the two mixers. These outputs are combined in the 0-deg. hybrid and altered by the hybrid's amplitude and phase imbalance. Vectorial addition of the mixer output sidebands results in enhancement of one of the sidebands and suppression of the other.

Due to imbalance, sideband suppression is not perfect. For example, a 1-deg. phase and 0.1-dB amplitude imbalance results in 40-dB sideband suppression. For a 30-dB suppression requirement, a combination of 1-deg. phase and 0.5dB amplitude imbalance is allowable.

The carrier frequency lies midway between the side-bands. Carrier suppression depends on mixer balance. For good modulator operation, the carrier signal should be at or below the suppressed-sideband level.

Rejection Testing

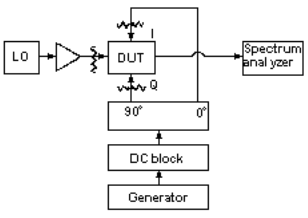
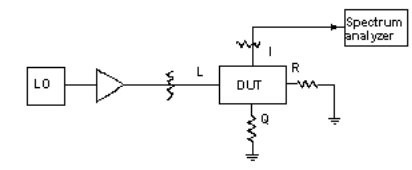
In the setup for testing carrier and sideband rejection/suppression (Fig.4), the low-frequency generator output is split into two signals at 0 and 90 deg. which are fed to the I and Q ports, respectively. The RF output is displayed on a spectrum analyzer. Carrier and sideband rejections can be read directly on the analyzer. Precaution is exercised by using a DC block to prevent and DC output from the low-frequency generator from biasing the mixers and causing a false measurement.

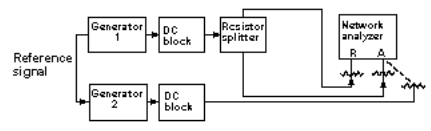
This test method places excessive contraints on the 90-deg. hybrid. Its amplitude and phase imbalance should be approximately 0.10 dB and 0.01 deg., respectively. An alternate technique is to use two generators to obtain equal amplitude signals that are 90 deg. out of phase. The two signal levels and phases can be adjusted using a setup that incorporates a network analyzer (Fig. 5). The output from generator l is split into two parts. One part is applied to the R port of the network analyzer and the other part is applied to the A port. The analyzer is then set to continuous-wave (CW) mode at the generator frequency using the front panel keys. The amplitude is adjusted to the required level, which can be read directly on the analyzer, and the amplitude and phase displays are normalized.

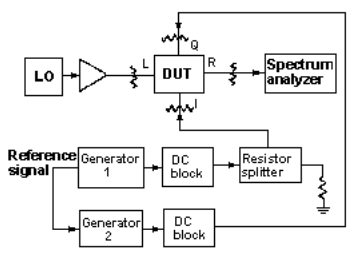
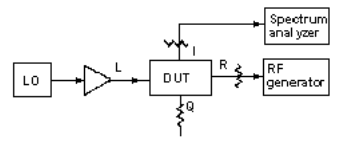
The signal at the A port is then removed and splitter port 2 is terminated at 50 Ω. The output of generator 2 is then applied to the analyzer A channel. The generator-2 output amplitude is adjusted to read 0 dB and the phase is adjusted to read 90 deg. Now the network analyzer is no longer needed. Port 1 of the resistive splitter is terminated at 50 Ω. The port-2 output is applied to the I port of the DUT and the output of generator 2 is applied to the Q port (Fig. 6). This technique provides a wide selection of I- and Q-port signal frequency and is limited only by the generator.

This setup can also be used to measure conversion loss. The absolute value of the amplitude of the higher sideband can be read from the spectrum analyzer. By knowing the attenuator loss on the RF port, conversion loss can be computed. The spectrum analyzer should be calibrated with a power meter to improve accuracy.

Isolation Measurements

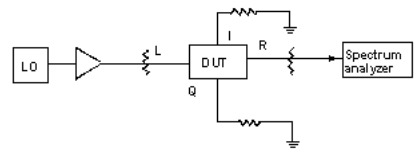
Isolation measurements are straightforward. The test set-ups for LO-to-RF (Fig. 7), LO-to-I or Q (Fig. 8), and RF-to-I or Q (Fig. 9) isolation incorporate a spectrum analyzer. High isolation is desirable in order to reduce filtering requirements. For LO-to-Q and RF-to-Q isolation measurements, the 50 Ω term on the Q port is interchanged with the spectrum analyzer cable on the I port.

In a typical demodulator, the LO and RF frequencies are very close to each other. For example, if the difference is 100 kHz, the third- and fifth-order IF products will appear at 300 and 500 kHz, respectively. Double-balanced mixers have excellent even-order product suppression, therefore the second- and fourth-order IF products are not of concern. A spectrum analyzer can be used to measure the third- and fifth-order products. Achievable levels for these products are typically -40 to -50dBc. Third and fifth order products in modulator applications can be measured using the test setup of Fig. 6.

If I- and Q-port circuits external to the I/Q network are DC-coupled, they will have a finite DC offset. The combination of this DC offset and the mixer offset will bias the mixer diodes and reduce the balance. Measurement of the DC offset is straightforward and is similar to mixer-offset measurement.

Modern Definition of Terms

I&Q

In-phase and quadrature-phase

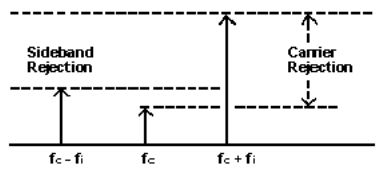
Carrier rejection

The amount of carrier measured in dB below the desired output signal when a coherent signal of equal amplitude and 90° phase difference is applied to the I&Q ports. This is shown in fig. 1. fc & fi, are carrier and IF (I-Port/Q-Port) frequency.

Sideband rejection

The amount of undesired sideband measured in dB below the desired sideband under the same conditions as the carrier rejection measurement.

Harmonic suppression

In a modulator, besides the undesired sideband and carrier, harmonic products of the IF combine with the carrier to produce undesired signals at RF as below.

The most important products are the third and fifth, fc ± 3fi and fc ± 5fi since they are very close to the desired sideband and almost impossible to filter.

For a demodulator, the harmonic products of interest are:

nfi

n = 3 and 5 are the products of most interest.

Conversion loss

For a modulator, conversion loss (C.L.), in dB, is defined as below C.L.(dB) = Input(I + Q) Power - Output RF Power of the dominant sideband

For a demodulator, it is defined as C.L.(dB) = RF Input Power - (I + Q) Output Power

Phase unbalance

The deviation from 90° of the phase angle difference of the I&Q port output signals.

Amplitude unbalance

For a demodulator, amplitude unbalance is the difference of the I and Q power.

Amplitude Unbalance = P_I(dBm) - P_Q(dBm)